Dik Açılı Üçgenin Kenar ve Açı Özellikleri Sunumları
-

8 5 yıl önceSilİlgili Yazı: Dik Açılı Üçgenin Kenar ve Açı Özellikleri
Dosya Adı: Üçgenlerin Açı ve Kenar Özellikleri Slayt Sunum Powerpoint PPTX
(Göster / Gizle) Sunum İçeriği: Düz metin (text) olarak..
1. Sayfa
ÜÇGENLER
2. Sayfa
İÇİNDEKİLERÜÇGENÜÇGEN EŞİTSİZLİĞİÜÇGENDE AÇI ÖZELLİKLERİÜÇGENİN YARDIMCI ELEMANLARIÜÇGEN ÇEŞİTLERİPİSAGOR BAĞINTISIALAN HESAPLAMASIÖRNEKLER(1-2-3)KAZANIMLARKAYNAKÇA
3. Sayfa
ÜÇGENDüzlemde doğrusal olmayan üç noktanın ikişer ikişer birleştirilmesiyle elde edilen geometrik şekle üçgen denir. ABCabcköşekenarİç açıdış açıstyle.visibilityppt_xppt_ystyle.visibilityppt_xppt_ystyle.visibilityppt_xppt_ystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilityppt_xppt_ystyle.visibilityppt_xppt_ystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibility
4. Sayfa
ÜÇGEN EŞİTSİZLİĞİBir üçgende bir kenarın uzunluğu diğer iki kenarın uzunlukları toplamından küçük, farkının mutlak değerinden büyüktür. Bu eşitsizliğe Üçgen Eşitsizliği denir.ABCcbab+c > a >|b-c|a+c > b> |a-c|b+a > c >|b-a|style.visibilityppt_xppt_ystyle.visibilityppt_xppt_ystyle.visibilityppt_xppt_ystyle.visibilityppt_xppt_ystyle.visibilityppt_xppt_ystyle.visibilityppt_xppt_ystyle.visibilityppt_xppt_ystyle.visibilityppt_wppt_h
5. Sayfa
ÜÇGENDE AÇI ÖZELLİKLERİÜçgenin dış açılarının ölçülerinin toplamı 360° dir.Üçgenin iç açılarının ölçülerinin toplamı 180° dir.style.visibilitystyle.visibilitystyle.visibilitystyle.visibility
6. Sayfa
Üçgende iki iç açının ölçüleri toplamı, bu açılara komşu olmayan dış açının ölçüsüne eşittir.style.visibilitystyle.visibilitystyle.visibility
7. Sayfa
Örnek 1ABC bir üçgen x , y, z birer dış açılarx+y-z= 160° ise z açısının ölçüsü kaç derecedir? CEVAP 1 X + Y + Z = 360° ( DIŞ AÇILARIN ÖLÇÜSÜNDEN ) -/ X + Y – Z = 160° 2Z=200 Z= 100° Bulunur. style.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibility
8. Sayfa
ÜÇGENİN YARDIMCI ELEMANLARIKenarortay Üçgenin bir köşesini karşı kenarın orta noktasına birleştiren doğru parçasına o kenara ait kenarortay denir. ABCVaVa: a kenarına ait kenarortaystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilityppt_xppt_y
9. Sayfa
ÜÇGENİN YARDIMCI ELEMANLARIYükseklik Üçgenin bir köşesinden karşı kenara veya karşı kenarın uzantısına çizilen dik doğru parçasına yükseklik denir.ABChahchbha: a kenarına ait yükseklikhb: b kenarına ait yükseklikhc: c kenarına ait yükseklikstyle.visibilityppt_xppt_ystyle.visibilityppt_xppt_ystyle.visibilityppt_wppt_hstyle.visibilityppt_wppt_hstyle.visibilityppt_wppt_hstyle.visibilityppt_wppt_hstyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibility
10. Sayfa
ÜÇGENİN YARDIMCI ELEMANLARIAçıortay Üçgenin bir köşesini, bu köşedeki açıyı ortalayacak biçimde karşı kenara birleştiren doğru parçasına açıortay denir.ABCstyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibility
11. Sayfa
üçgen çeşİTLERİ Dar Açılı Üçgen Dik Açılı ÜçgenGeniş Açılı Üçgen Kenarlarına göreEşkenar Üçgenİkizkenar ÜçgenÇeşitkenar ÜçgenAçılarına görestyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibility
12. Sayfa
AçilarINA GÖRE ÜÇGENLERDar Açılı Üçgen Açıları 90° den küçük olan üçgenlere dar açılı üçgen denir.Dik Açılı Üçgen Bir açısı dik (yani90°) olan üçgene denir.Bu üçgenlerde yükseklik dik kenarlardan biridir.En uzun kenarına hipotenüs denir.Geniş Açılı Üçgen Açılarından biri 90°den büyük olan üçgenlerdir. Sadece bir tek açısı geniş açı olabilir. Tabana ait yükseklik tabanın uzantısı ile kesişir.style.visibilitystyle.visibilitystyle.visibility
13. Sayfa
KenarlarINA GÖRE ÜÇGENLEREşkenar Üçgen Tüm kenarları eşit olan üçgen olup iç açılarının her biri 60°'dir. Tabanlara indirilen dikmeler hem açıortay hem de kenarortaydır.İkizkenar Üçgen İki kenarı eşit olan üçgenlerdir. Ayrıca iki açısı birbirine eşittir. Eşit olmayan kenara indirilen dikme hem açıortay, hem kenarortay özelliği gösterir.Çeşitkenar Üçgen Her kenarının uzunluğu ve açısı farklı olan üçgenlerdir.style.visibilitystyle.visibilitystyle.visibility
14. Sayfa
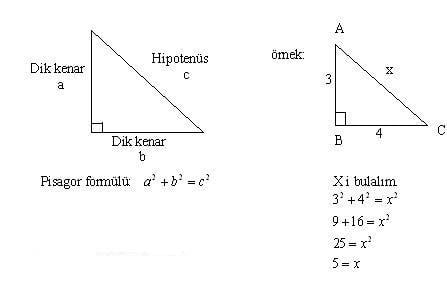
pİsaGOR BAĞINTISIBir dik üçgenin dik kenarlarına 'a' ve 'b' dersek hipotenüs'ün karesi bu kenarların uzunluklarının karelerinin toplamına eşittir. Buna PİSAGOR TEOREMİ denir . ABCcbastyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibility
15. Sayfa
PİSAGOR BAĞINTISININ GÖRSEL AKTARIMI style.visibilitystyle.visibility
16. Sayfa
Alan hesaplamasIBir üçgenin alanı, taban ve tabana ait yüksekliğin çarpımının yarısıdır.ABCaALAN = ha.a 2hastyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilitystyle.visibilityppt_wppt_hstyle.visibilityppt_wppt_hstyle.visibilityppt_wppt_hstyle.visibilitystyle.visibilitystyle.visibility
17. Sayfa
Örnek 2 CEVAP 2 style.visibilitystyle.visibilitystyle.visibilitystyle.visibility
18. Sayfa
ÖRNEK 3 CEVAP 3style.visibilitystyle.visibilitystyle.visibilitystyle.visibility
19. Sayfa
KAZANIMLARÜçgende kenarortay, açıortay ve yüksekliği inşa eder.Üçgenin kenar uzunlukları ile bu kenarların karşısındaki açıların ölçülerini ilişkilendirir.Pisagor bağıntısını oluşturur; ilgili problemleri çözer.Üçgenin iki kenar uzunluğunun toplamı veya farkı ile üçüncü kenarının uzunluğunu ilişkilendirir.style.visibilitystyle.visibilitystyle.visibilitystyle.visibility
20. Sayfa
KAYNAKÇAİNTERNET SİTESİ MEB KONU ANLATIM SİTESİwww.youtube.com/watch?v=-N27KbJZlB8http://www.matematikciler.orgrstyle.visibilitystyle.visibility
21. Sayfa
FATMA ÖZEKİN 130403103 2-A İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ HAZIRLAYAN rstyle.visibility
22. Sayfa
r
İndir / Download : 80_ucgenlerin-aci-ve-kenar-ozellikleri.pptx
Yorumlar
| Sıra | Adı | İndirilme |
|---|---|---|
| 01 | Tutanak Örnekleri | 23485 |
| 02 | Türemiş Kelime | 20494 |
| 03 | Yüksek Lisans Referans Mektubu Örneği | 18862 |
| 04 | Tahliye Taahhütnamesi | 12522 |
| 05 | Yıllık İzin Dilekçe Örneği | 12269 |
| 06 | Leonardo da Vinci | 12039 |
| 07 | Olimpiyat | 11784 |
| 08 | Saf Şiir | 11643 |
| 09 | Niyet Mektubu Nasıl Yazılır | 10899 |
| 10 | Niyet Mektubu | 10793 |
| 11 | Dış Kuvvetlerin Oluşturduğu Yer.. | 10556 |
| 12 | Tutanak Nasıl Yazılır | 10500 |
| 13 | Ayasofya Tarihçesi | 9056 |
| 14 | Rönesans Ve Reform | 8811 |
| 15 | İnisiyasyon | 8681 |
| 16 | Savunma İstem Yazısı | 8087 |
| 17 | Öğrenci Kopya Tutanağı | 7784 |
| 18 | Akademik Referans Mektubu Örneği | 7225 |
| 19 | Sanat | 7087 |
| 20 | Türkiyede Görülen İklim Tipleri | 7008 |
| 21 | Referans Mektubu Örnekleri | 6652 |
| 22 | Empresyonizm Sanatı ve Sanatçıları | 6338 |
| 23 | 2. Sınıf Sihirli Sözcükler Konu.. | 6210 |
| 24 | Sorumluluk | 6145 |
| 25 | Teslim Tesellüm Tutanağı Örneği | 6101 |
| 26 | İlköğretim Haftası | 5849 |
| 27 | Muvafakatname | 5546 |
| 28 | Bilimsel Araştırma Basamakları | 5543 |
| 29 | Masal | 5334 |
| 30 | Maddenin Özellikleri Çalışmaları | 5104 |